Havel-Hakimi Illustrated

Havel-Hakimi algorithm is an algorithm which can verify whether there exists a simple graph for given degree sequence. Before we dive into the actual algorithm lets revisit some of the key terms: simple graph and degree sequences.

 1. What is Simple Graph?

A simple graph is an undirected, unweighted graph with no self loops and no multi-edges.

2. Degree Sequences

A degree of a vertex i, is number of edges incident on i with self loops counted twice. Degree sequences is the arrangement of degree in non-ascending or non-descending order.

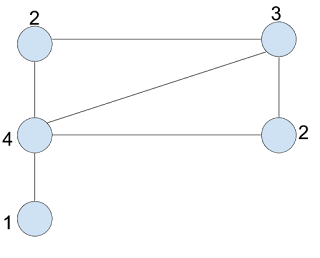Figure 1:- Degree Sequences: Graph with degree sequence (4, 3, 2, 2,1)

 3. Havel-Hakimi Algorithm

1.  Put degree sequence in non-ascending order
2.  Remove highest degree, k
3.  Subtract 1 from next k entries in degree sequence
4.  Repeat step 1, 2, 3 & stop until
1.  If we get all zero entries -> simple graph exist
2.  If we get at least one negative entry -> simple graph does not exist
3.  If no enough entries -> simple graph does not exist

For example: Let us consider the degree sequence (4, 3, 2, 2, 1)
(4, 3, 2, 2, 1)
Highest degree, k = 4
Subtract 1 from the next k entries degree sequence excluding 4.
(2, 1, 1, 0)
Highest degree, k = 2
Subtract 1 from the next 2 entries
(0, 0, 0) -> All zeros
Therefore, simple graph exist for the degree sequence (4, 3, 2, 2, 1).