Havel-Hakimi Illustrated
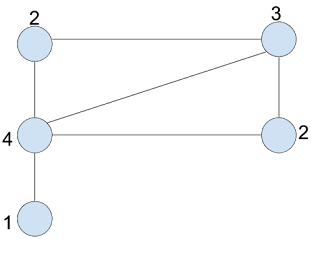
Havel-Hakimi algorithm is an algorithm which can verify whether there exists a simple graph for given degree sequence. Before we dive into the actual algorithm lets revisit some of the key terms: simple graph and degree sequences. 1. What is Simple Graph? A simple graph is an undirected, unweighted graph with no self loops and no multi-edges. 2. Degree Sequences A degree of a vertex i, is number of edges incident on i with self loops counted twice. Degree sequences is the arrangement of degree in non-ascending or non-descending order. Figure 1:- Degree Sequences: Graph with degree sequence (4, 3, 2, 2,1) 3. Havel-Hakimi Algorithm Put degree sequence in non-ascending order Remove highest degree, k Subtract 1 from next k entries in degree sequence Repeat step 1, 2, 3 & stop until If we get all zero entries -> simple graph exist If we get at least one negative entry -> simple graph does not exist If no enough entries -> simple graph doe